Properties of European Options: Put-Call Parity

Options and Futures

Zhiyu Fu

Review of Option Payoffs

• Long underlying assets:
  • Long call
  • Short put

• Short underlying assets:
  • Short call
  • Long put

Put-Call Parity

\[C\] \[\large +\] \[ -P\]

\[ C - P\]

Put-Call Parity

\[S_0\] \[\large +\] \[ -K e^{-rT}\]

\[ C - P\]

Synthetic Long: Creating a Forward at \(K\)

\[\Large C - P = S_0 - K e^{-rT}\]

• Definition: Long a call and short a put at the same strike price and same expiration date is equivalent to borrowing to buy the underlying asset.

• Conditions:

  • Non-dividend paying stock
  • Not for American options (why?)
  • No transaction costs/heterogeneous tax treatment/other frictions

• Various versions:

  • \(S_0 - C = K e^{-rT} - P\)
  • \(S_0 + P = C + K e^{-rT}\)

• What happens if the parity does not hold? Buy low, sell high.

Synthetic Shorting

Synthetic shorting: long put + short call

• Do you need margin for it?

• Does it matter for the stock price?

  • Not directly: You don’t sell the stock directly
  • But the market makers will sell
    • To hedge a synthetic long position from options
  • “Gamma squeeze” in meme stocks
    • Long short dated options so the market makers have to buy the stock to hedge

Synthetic Long + Synthetic Short: The Box Spread

• Synthetic long at the lower strike \[C^L - P^L = S_0 - K^L e^{-rT}\]
• Synthetic short at the higher strike \[-(C^H - P^H) = -(S_0 - K^H e^{-rT})\]
• The difference is the box spread \[ \underset{\text{Initial Investment}}{\underbrace{C^L - P^L - (C^H - P^H)}} = \underset{\text{Riskfree Payoff}}{\underbrace{(K^H - K^L)e^{-rT}}} \]
• We created a riskfree bond out of options!

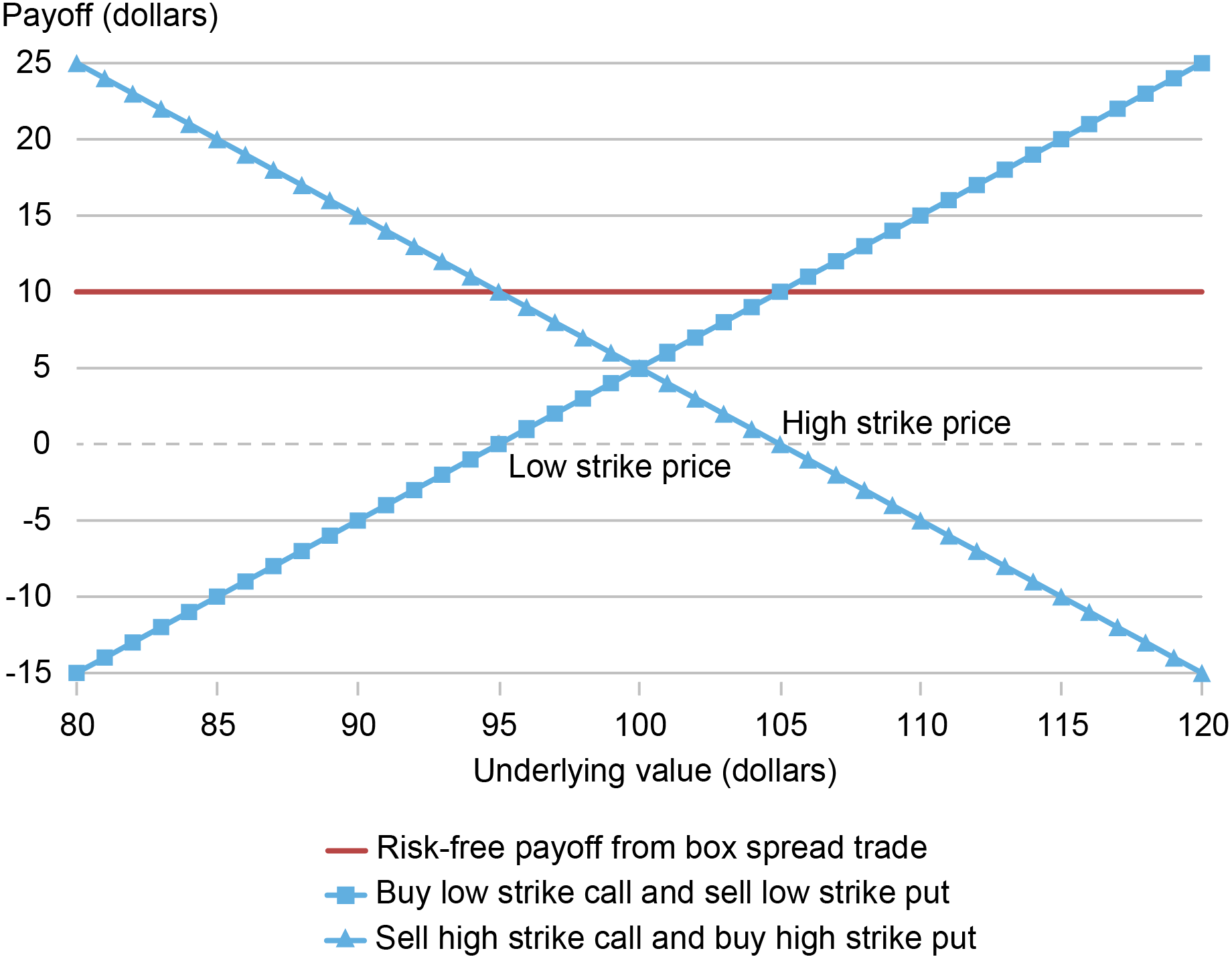
Box Spread

Why we want to do that?

1. Higher returns than government bonds
2. Potential tax benefits (debatable)

• Instead of income tax, you pay capital gain tax
• May violate the conversion transaction rule

3. Higher flexibility than SOFR (secured repo)

• See the discussion by CME

4. You can invest in it simply with an ETF

Option Bounds

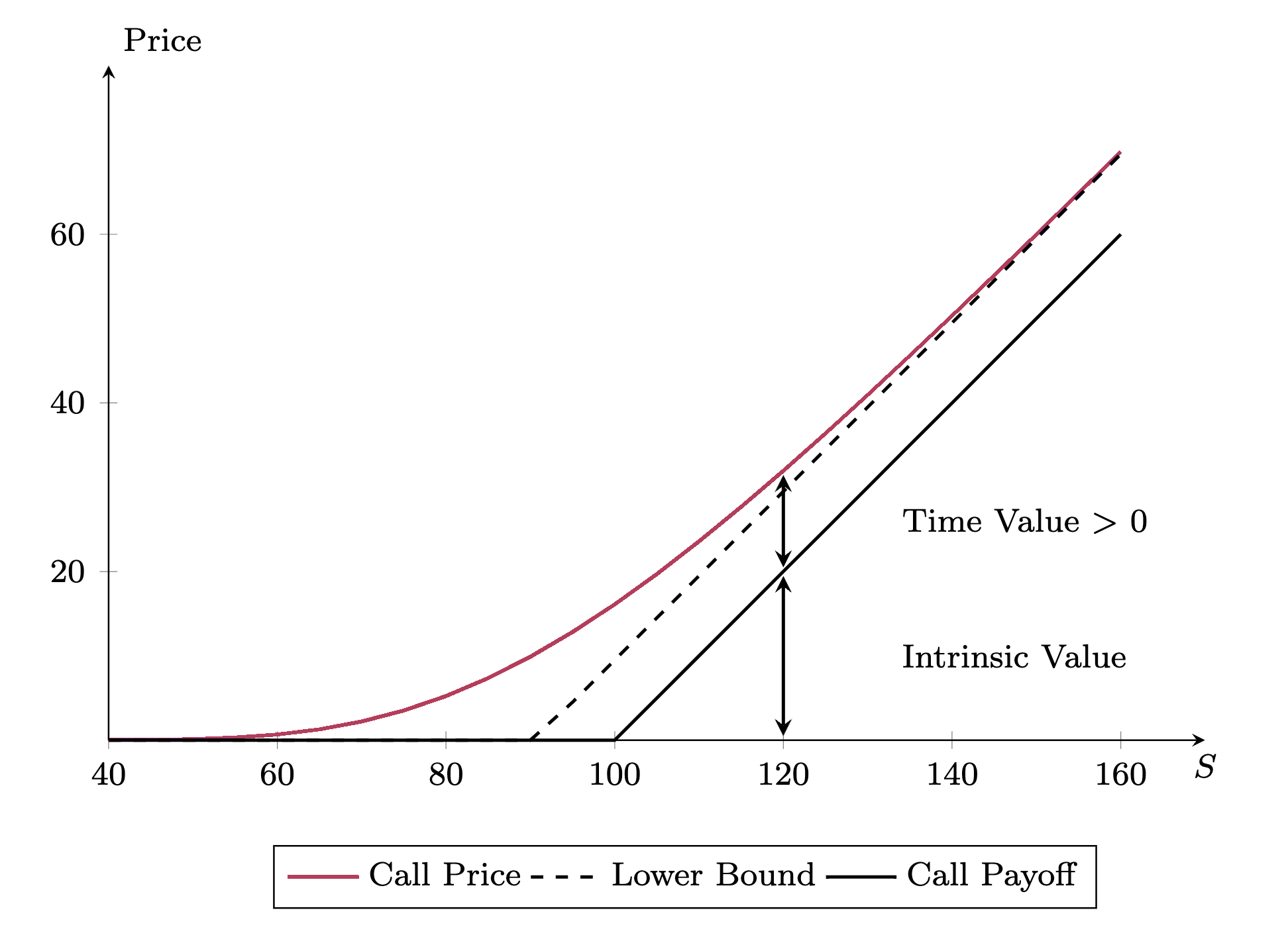
The Lower Bound of European Call Options

Labels indicating current prices rather than future payoffs

Two observations from the diagram: 1. The payoff of the call option is positive \(\implies\) \[C > 0\] 2. The payoff of the call option (solid) is better than borrow to buy the stock (dashed) \(\implies\)

\[C > S_0 - K e^{-rT}\]

• From the put-call parity, knowing the put price \(P\) is positive, we have

  \[C = S_0 - K e^{-rT} + P > S_0 - K e^{-rT}\]

Taken together, we have the lower bound of the call option: \[C > \max(0, S_0 - K e^{-rT})\]

What happens if the lower bound is violated?

• It is a violation of the put-call parity:

\[C < S_0 - K e^{-rT} \implies \underset{\text{Buy low}}{\underbrace{C - P}} < \underset{\text{Sell high}}{\underbrace{S_0 - K e^{-rT}}}\]

How do we implement this?

Now:

• Buy the call option at \(C\)
• Sell the put option at \(P\)
• Save \(K e^{-rT}\) at risk-free rate \(r\)
• Short-sell the stock at \(S_0\)

Net gains: \(S_0 - K e^{-rT} - (C - P) > 0\)

At maturity:

• If \(K < S_T\), exercise the call to buy the stock at \(K\) using the cash saved, return to the short-sell position
• If \(K > S_T\), buy the stock at \(K\) from the put holder using the cash saved, return to the short-sell position
• Terminal payoff: \(0\)

The Convergence of Call Price to the Lower Bound

Under regular conditions, the call price converges to the lower bound when it’s deep.

• Deep out of the money: \[K \gg S_0 \to 0 \implies C \to 0\]

• Deep in the money: \[K \ll S_0 \to \infty \implies C \to S_0 - K e^{-rT}\]

  • From the put-call parity, \[C = S_0 - K e^{-rT} + P\]
  • When \(S_0 \gg K\), \(P \to 0\)
  • Implication: European call options for non-dividend paying stocks always have a positive time value!

Call price as a function of the current stock price

The Upper Bound of European Call Options

Labels indicating current prices rather than future payoffs

The payoff of a call option is less than the payoff of the stock itself.

\[C < S_0\]

What happens if the upper bound is violated?

Sell a call and use the cash to buy the stock

Bounds on European Put Options

Labels indicating current prices rather than future payoffs

1. The payoff of the put option is positive \(\implies P > 0\)
2. The payoff of the put option (solid) is better than shorting the stock (dashed) \(\implies\)

\[P > K e^{-rT} - S_0\]

• From the put-call parity, knowing the call price \(C\) is positive, we have

  \[P = K e^{-rT} - S_0 + C > K e^{-rT} - S_0\]

3. The payoff of the put option is at most \(K\), \(P < K e^{-r T}\)

Taking together, we have the bounds on the put option: \[ \max(0, K e^{-rT} - S_0) < P < K e^{-rT}\]

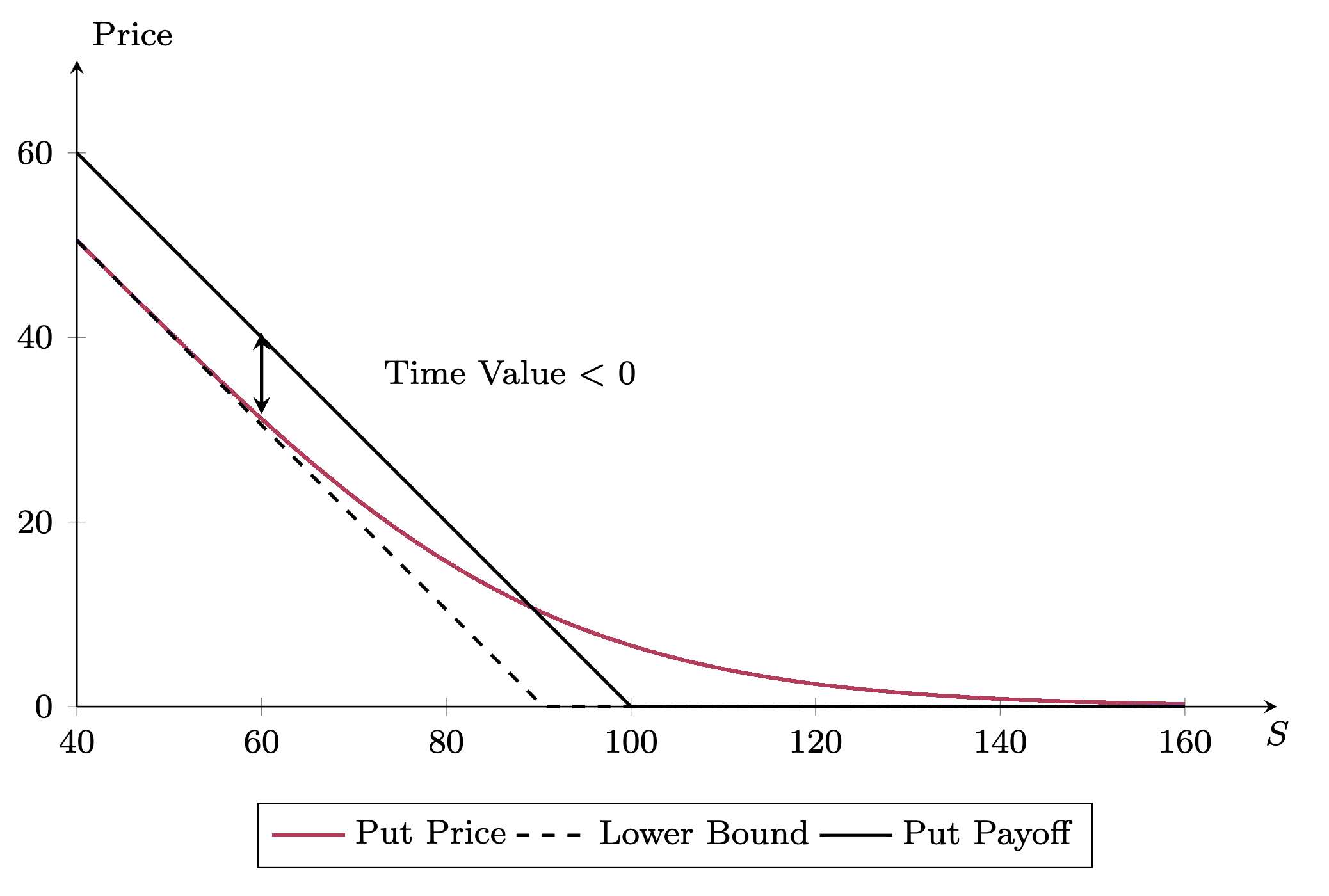
The Convergence of Put Price to the Lower Bound

Under regular conditions, the put price converges to the lower bound when it’s deep.

• Deep out of the money: \[K \ll S_0 \to \infty \implies P \to 0\]

• Deep in the money: \[K \gg S_0 \to 0 \implies P \to K - S_0 e^{-rT}\]

  • From the put-call parity, \[P = K - S_0 e^{-rT} + C\]
  • When \(S_0 \ll K\), \(C \to 0\)
  • Implication: A deep ITM put will have a negative time value

Put price as a function of the current stock price