Time Values, American Options, and Dividends
Options and Futures
Zhiyu Fu
What Affects the Option Price?
- Use this binomial tree calculator to explore the effect of the parameters on the option price
- Take the at-the-money call option for one year and change the following parameters and see how the option price changes:
| Parameter | European Call | European Put |
|---|---|---|
| current stock price S_0 | + | - |
| strike price K | - | + |
| volatility \sigma | + | + |
| risk-free rate r | + | - |
| time to maturity T | + | ? |
The Time Value of Non-Dividend Paying European Options
The time value of an option is the difference between the option price and the intrinsic value: C - \max\{S_0 - K, 0\} There are two components of the time value:
The value from the uncertainty: the stock price could move in the favorable direction
- The longer the time to maturity, the more uncertainty, the more valuable are the options, both calls and puts
The value due to the embedded leverage in options
- Calls: Equivalent to a dynamically hedged position of long stock and short bond
- The longer is the period, or the higher is the risk-free rate, the less present value of the bond given the same future payoff, and hence the higher value of the embedded leverage in a call
- Puts: Equivalent to a dynamically hedged position of short stock and long bond
- The longer is the period, or the higher is the risk-free rate, the less present value of the bond, and the lower value of the embedded leverage in a put
- Calls: Equivalent to a dynamically hedged position of long stock and short bond
Two components work in the same direction for calls but opposite directions for puts!
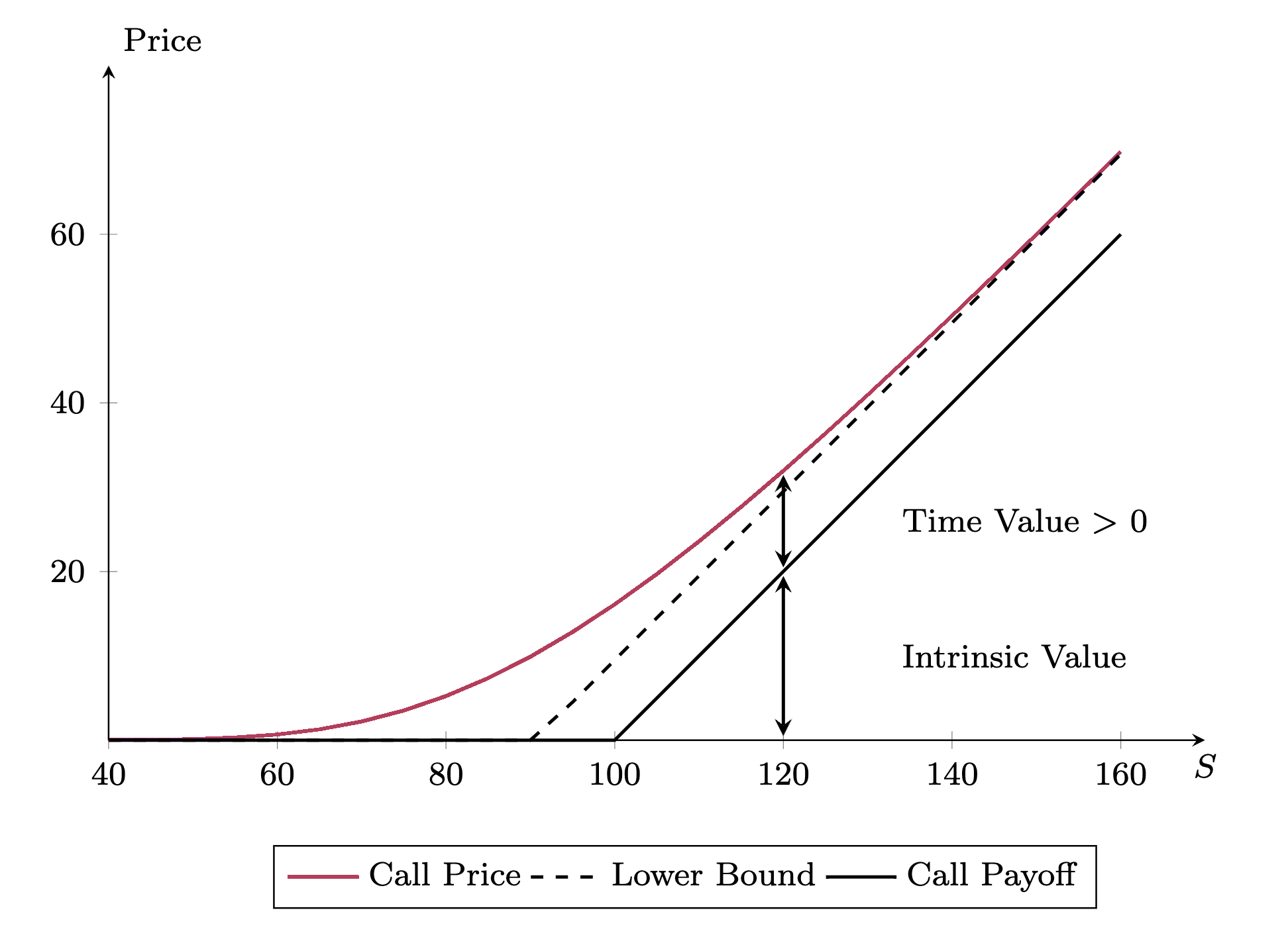
The Lower Bound of European Calls and Puts and the Time Value
- Call options always have a positive time value:
\small \begin{aligned} C &> \max\{S_0 - K e^{-rT}, 0\} \\ \implies C &> \max\{S_0 - K, 0\} \end{aligned}
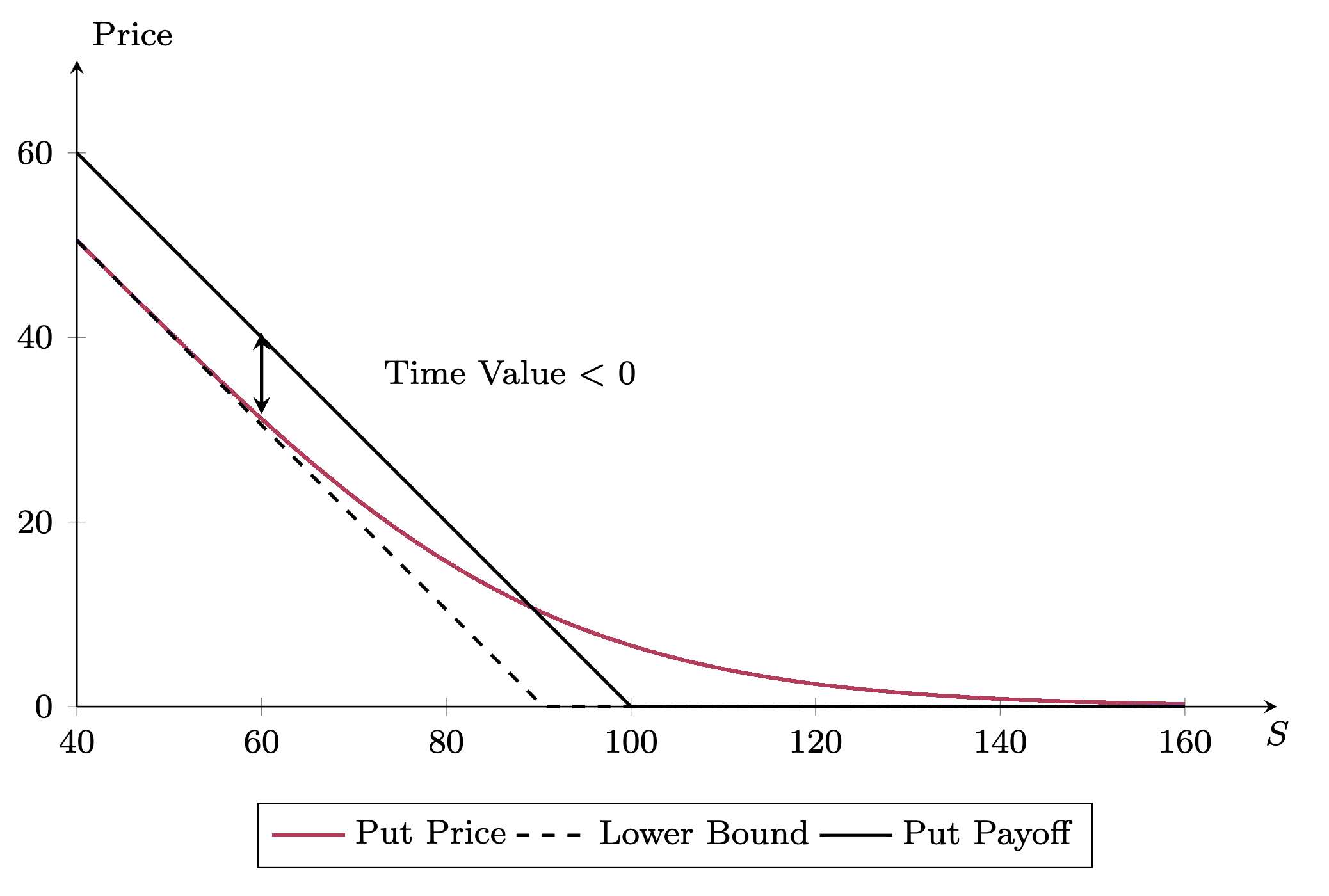
- Put options may have a negative time value:
\small \begin{aligned} P &> \max\{K e^{-rT} - S_0, 0\} \\ \nRightarrow P &> \max\{K - S_0, 0\} \end{aligned}
American Options
- American options can be exercised at any time before the maturity
- To price the american options, we only need an additional step in the binomial tree
- Step 1: Calculate the risk-neutral probability
- Step 2: From the leaves, calculate option value without early exercises P^E_i P^E_{i} = (P^E_{iu} * q + P^E_{id} * (1-q)) e^{-rΔt} where P^E_{iu} and P^E_{id} are the option values at the up and down nodes of the node i
- Step 2.5: The American option price is the maximum of the option price without early exercise and the exercise value (using American put option as an example) \begin{aligned} P^A_{i} &= \max\{P^E_{i}, K - S_i\} \end{aligned}
- Step 3: Moving backward in time
Example: European Call
Example: American Call
Example: European Put
Example: American Put
Properties of American Options
- Because American options have all the benefits of European options, they should be at least as valuable as European options
- American calls:
- For non-dividend paying stocks, because calls always have a positive time value, it is always not optimal to exercise early even if it is feasible
- You should always sell the American call rather than exercise it
- American calls effectively have the same price as European calls
- American puts:
- Because the time value of European puts can be negative, it can be optimal for American puts to be exercised early
- The time value of American options is always positive
- The longer the time to maturity, the more valuable are American options, both calls and puts
Options on Dividend Paying Stocks
- The treatment is the same as futures with holding benefits and costs
- When replicating the payoff of options using the stock and bond, we need to adjust the bond amount by the present value of the dividends
- The put-call parity is adjusted by the present value of the dividends: C - P = S - PV(D) - K e^{-rT} where PV(D) is the present value of the dividends
- With dividends, it can be optimal to exercise American options early before the dividends are paid so stock price is higher
- Hence, American call options are more valuable than European call options on dividend-paying stocks